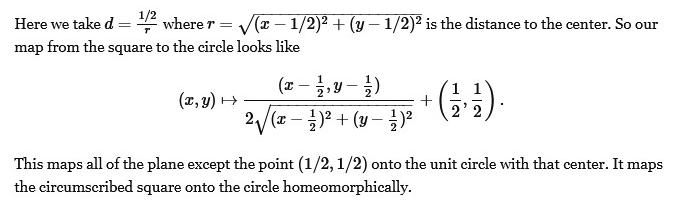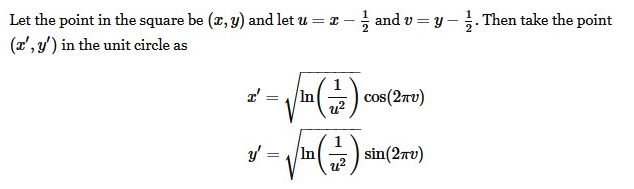Thank you. I will need a better understanding of mathematics to completely grasp the idea, but I see the direction that it goes toward.
So thank you again . . . although I still feel confused (and I recognize that it’s beyond the scope of a forum post to teach me advanced mathematics).
I picture the idea as a “one to one” correspondence of points between a circle and a square.
Yet any square and any circle contains an infinite number of points regardless of how big or small these shapes are.
People generally don’t grasp the ideas behind infinity, as most people think of it as a very large number . . . when–in reality–no number (no matter how large) is, somehow, “closer to infinity” by virtue of being a big number.
This is because any number–no matter how large–has an end, and by having an end it lacks the quality of endlessness that defines infinity.
This has odd implications that are counter-intuitive, like the hotel with infinite rooms that are all occupied, which also seems relevant to this squaring the circle business.
I would like you to imagine that you are the concierge in a hotel with an infinite number of rooms, and each room is occupied. Also, in order to stay in this hotel, there’s a rule that you have to be nice to your neighbors, or else you get evicted.
Well, a wealthy businessman comes in and says that he desperately needs a room, and he’s willing to offer you a very generous bribe in order to get him a place to sleep.
If your infinite hotel is completely occupied, then you might suspect that there are no rooms available.
Yet this isn’t true!!!
You accept the bribe, you send him to the first room, and he has to ask the occupant to relocate to the second room . . . and the occupant in the 2nd room then has to relocate to the third room, where this occupant nicely leaves and relocates to the 4th room, and so on.
Because this process goes on endlessly, nobody does without a room except when they spend five minutes crossing the hallway to talk to the occupant of the next higher room, and nobody ever has to check out of this hotel.
And this could be done as often as you want! Even though every room is occupied in the infinite hotel, you could still endlessly and constantly send more guests for rooms without ever running out . . . even though every room is occupied (Am I the only one, or does mathematical logic sometimes seem to get wierd and a little strange?)
This correspondence between the points of a square and the points of a circle seem similar to me, so I obviously don’t understand it. I’ll do my research, ask some math professors at the college, and I’ll get back to you.