Got a question.
I understand why a rotating wheel moves forward. I understand why two wheels connected by an axle moves forward. I don’t understand why rotational motion of four wheels connected by two axles cause a chassis to move in a forward direction.
What type of force caused by the motion is exerting forward motion on the chassis?
The best I can think of is that the rotation of the axle on the chassis produces a forward moment of force at the point of connection.
Engine excerts torque on the axle, which transfers the torque to the wheel. Due to the weight of the vehicle, the wheels will experience friction on the ground. When torque is applied, the wheel will experience a force from the contact point with the ground (and the ground will experience a force from the wheels). If this force is lower than what the static friction between the wheel and the ground can hold, AND the axle is free to rotate, these forces will translate to a forward motion of the vehicle. Since the axle is forced to rotate due to the engine, the axle will cause tension, and the only way for this tension to be released is for the wheel to turn, and since the wheel cannot slip relative to the ground, the vehicle has to move forward.
6 Likes
Try adding friction to your model (friction between the tires and the road). That should solve your problem/dilemma.
go with @Get_off_my_lawn’s answer above.
eta: A simple way to think about it; if you have 0 friction, you can’t accelerate (not with tires anyway); and turning is also an acceleration (and so is slowing down).
0 friction is bad if you are in a car; as anyone who has lived anywhere cold already knows from driving on ice.
4 Likes
This I where I lose the explanation. What contact is involved in this translation? Is it the contact of the spinning axle with the spine of the chassis that creates the forward motion?
Fuck. I “know” this makes perfect sense, but I don’t get it.
All that tension and friction force the wheel to turn. And where else is the rest of the vehicle going to go?
But, for example: if you have a unicycle … and the axle is rigidly fixed to the rest of the vehicle, then the rest of the vehicle will turn with the wheel.
Then we remove the ridged connection between the axle and the rest of the vehicle … then is it correct that the vehicle goes clinkity clunkity down the road kind of bobbing up and down on the rotating axle? Is that the right intuitive understanding?
Imagine a car driving on a thin layer of fine sand (or a dirt road). Rotating a rubber tire next to the ground shoots grains of sand in one direction (a force); lets call that direction “out the back”. From Newton’s 3rd law there must be an force of equal magnitude in the opposite direction (towards the front); that is what moves the car forward. It is just the conservation of momentum.
Rockets work the same way, but instead of shooting sand out the back, they shoot highly compressed air (from some chemical reaction, like combustion).
What makes it weird is when the tire is on a nice road where the motion “out of the back” isn’t macroscopic (it will appear as heat, which isn’t easy to see), but the forward motion is very obvious.
1 Like
It might also help to simplify the whole thing. Let’s consider a bicycle instead. The principle will remain the same. Pressing the pedals will excert torque on them, which is transferred to the back wheel through the chain. The torque on the rim of the wheel pushes against the ground, but the wheel is stopped from moving freely due to friction. This is because the wheel pushes against the ground with a backward-directed force. Newton’s third law (if two bodies exert forces on each other, these forces have the same magnitude but opposite directions) dictates that the ground pushes back on the wheel. The ground is very hard to move, but there is very little to restrain the bicycle from moving forwards. Therefore, the counterforce from the ground pushes the bike forward.
Another way to look at it would be to look at it in reverse. Place the bike on the ground, and stand beside it. Now move the bike backwards. The friction between the wheels and the ground forces the wheels to turn. The backwards motion of the wheels also makes the chain move, and the chain moves the pedals. Now, while still moving the bike backwards, place your hand on one of the pedals. You will feel a force applied to your hand from the pedal, making your hand move. So, the force at the rim of the wheel translates through the mechanics of torque on the axle through a linear pull on the chain, and then again to torque on the pedals, which excerts a force on your hand. When riding forward on the bike, you have the same process, only reversed.
A third way: Place the bike upside down, as if you were going to service it. Place you hand on the back wheel, and let someone else turn the pedals with their hands. When the wheel starts to rotate, you will feel a force on your hand that moves your hand in the backwards direction, seen from the bike. When the bike is right side up, exactly the same thing happens, only with the ground instead of your hand. The bike moves the ground ever so slightly backwards, and is given some non-zero momentum. Due to the big mass of the earth, the change in velocity is negligible. On the bike, however, the momentum translates to speed, as the mass is negligible compared to the earth.
Perhaps it is the translation of torque (rotational motion) to linear force (forward motion) that confuses you? Or is it perhaps how friction ensures a counter force on the car or bike?
1 Like
And yet another way of looking at it. Consider the folling device for converting rotational motion to linear motion:
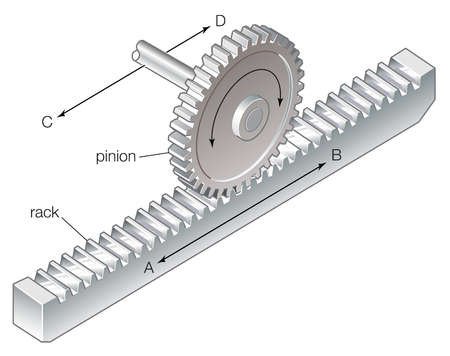
Here we have a cog wheel that interacts with a linear device with notches. The notches in the cog wheel fits with the notches in the linear device. If the axle on the cog wheel is held in place, the cog wheel can not move in the C<->D direction. Now imagine that the linear device moves in the A<->B direction. The notches in the linear device grabs the notches in the cog wheel, and forces it to rotate, and hence also the axle. Now turn it around. If we force the axle to turn, we force the cog wheel to turn, and the notches in the cog wheel grab the notches in the linear device, forcing the linear device to move in the A<->B direction.
For the next step, imagine that the linear device is fixed to the ground, and the axle is free to move in the C<->D direction. Forcing the axle to turn means the cog wheel will turn, and the notches on the rim of the cog wheel will grab the notches in the linear device on the ground. The cog wheel notches pushing against the notches on the linear device will now push the wheel and the axle along C<->D. If the cog wheel rotates clockwise, it will move in the D direction. If it rotates counterclockwise, it will move in the C direction.
Next, reduce the size of the notches to match the microscopic size of the irregularities to match the size of the irregularities in the rubber of a car wheel, and the irregularities on the linear device to match the irregularities of the ground. Also let the irregularities have random sizes and spacings. The notches will not match up perfectly, but there will still be notches that are available to grab each other, and transfer the force that convert rotational motion to linear motion.
4 Likes
Thank you. That was helpful. I have a follow up question regarding magnetic induction of electricity.
Suppose we have a horse shoe magnet (a U - magnet). And the distance between the north and south pole is, say, 1 foot (it’s pretty big).
We have a solenoid measuring .8 feet diameter. We pass the solenoid between the U of the magnet.
What type of current is induced in the solenoid and in what direction?
Fixed that for you.
If the circuit is open: None.
If the circuit is closed: A current will be induced so as to oppose the motion of the coil. The direction and amperage of the current will depend on the magnetic field between the poles, the orientation of the solenoid, and the speed it is inserted with. The exact current will depend on the number of turns on the solenoid and the time derivative of the magnetic flux through the solenoid. Electromagnetic induction - Wikipedia
3 Likes
Here Ratty: I know all these guys are just being mean to you. They are writing out logical explanations that you just can’t understand. This is the simple version… https://www.youtube.com/watch?v=mBlOX83txt8 (Brought to you by Tin Man’s younger brother, 'Sam.")
